MIIS Most Interesting Integer Sequences, chosen from OEIS.

---

A096179 - Matthew Vandermast, 2004/06/19

T(n, k) is the smallest positive integer having at least k of the first n positive integers as divisors.

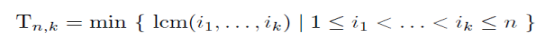
Note that the set of all tuples of the form { (i₁, ... , i_k) | 1 ≤ i₁ < ... < i_k ≤ n } are the combinations of {1, 2, ... n} of length k, enumerated by the binomial coefficient n over k.

The significance of this sequence lies in the fact that it is a natural generalization of the least common multiple of the initial section of the integers, which is the exponential of the second Chebyshev function, an important function in the study of the prime number.

• n = 1:
  T(1, 1) = lcm{1} = 1.
• n = 2:
  T(2, 1) = lcm{1} = 1.
  T(2, 2) = lcm{1, 2} = 2.
• n = 3:
  T(3, 1) = lcm{1} = 1.
  T(3, 2) = min{ lcm(1, 2), lcm(1, 3), lcm(2, 3) } = min{2, 3, 6} = 2.
  T(3, 3) = min{ lcm(1, 2, 3) } = min{ 6 } = 6.

Now let Maple compute the triangle for some rows n.

# Generate all the combinations of { 1, ..., n } of length k,
# compute their least common multiple and choose the smallest one.

A096179_row := proc(n) local k; 
seq(min(seq(lcm(op(s)),s=combinat[choose](n,k))),k=1..n) end:

# Test for n = 1, 2, ..., 16:

seq(A096179_row(i),i=1..16);

This implementation is useful only for small n. For larger n Pari is better suited and much faster.  The implementation is due to M. F. Hasler.

\\ Generate all the combinations of { 1, ..., n } of length k,
\\ compute their least common multiple and choose the smallest one.

A096179(n, k) = { 
   my(m = lcm(vector(k, i, i))); 
   forvec(v = vector(k-1, i, [2, n]), m > lcm(v) & m = lcm(v), 2); 
   m
} 

\\ Test for n = 1, 2, ..., 22:

for(n = 1, 22, for(k = 1, n, print(A096179(n, k))))

The following overview is based on the concept of a fingerprint of an integer triangle, as used on the Encyclopaedia Combinatorial Triangles ECT. Note the definitions given there. For instance to exclude trivial cases '1' is generally excluded from the computation of the gcd of rows for n > 1.

MIIS Most Interesting Integer Sequences, chosen from OEIS.