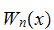Additive decompositions of classical numbers via the Swiss-Knife polynomials.

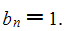
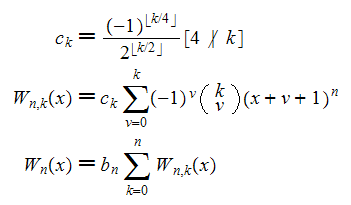
The additive decompositions of the Euler, Bernoulli, Genocchi, Springer and tangent numbers given below can of course also be interpreted as algorithms for computing these numbers. It is especially interesting to compare them with the algorithms used by Kwang-Wu Chen in Algorithms for Bernoulli numbers and Euler numbers, Journal of Integer Sequences, Vol. 4 (2001), Article 01.1.6, Theorem 3. Chen's algorithms use rational arithmetic (see the computational triangles following theorem 3) whereas our algorithms use only integer arithmetic.

Swiss-Knife polynomials 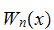$W_{n}(x)$ with MATH MATH

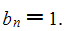
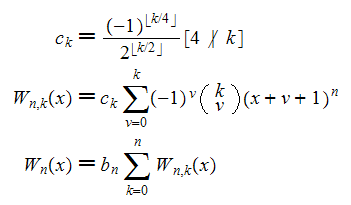
Euler number 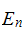$E_{n}$ with MATH MATH

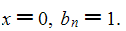
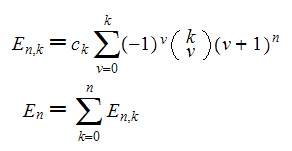
Tangent number 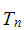$T_{n}$ with MATH MATH

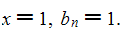
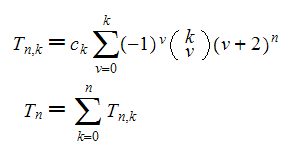
Springer number 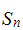$S_{n}$ with MATH MATH MATH

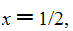
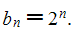
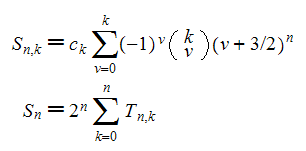
Genocchi number 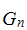$G_{n}$ with MATH MATH MATH

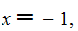
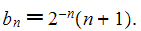
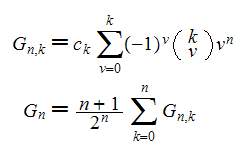
Bernoulli number 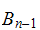$B_{n-1}$ with MATH MATH
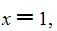
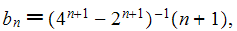
(note the shift of n, n > 0) MATH

previous Swiss-Knife polynomials

Maple Code

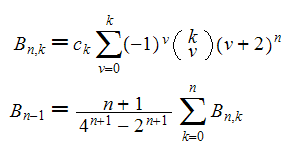
The following little routine computes five of the most famous sequences of special numbers in mathematics in 16 lines, using nothing else but the power function and the binomial coefficients.

SwissKnifeDecompositions := proc(type, n) local W,w,x,y;

     W := proc(n,k) local v, pow;
        pow := (a,b) -> if a = 0 and b = 0 then 1 else a^b fi;
        if irem(k+1,4) = 0 then 0 else (-1)^iquo(k+1,4)*2^(-iquo(k,2))*
           add((-1)^v*binomial(k,v)*y*pow(x+v+1,n),v=0..k)
        fi end;

      w := proc(n) local k;
           print(seq(W(n,k),k=0..n)); add(W(n,k),k=0..n) end;
 
      if type = "eul" then x := 0; y := 1; w(n)
      else if type = "tan" then x := 1; y := 1; w(n)
      else if type = "spr" then x := 1/2; y := 2^n; w(n)
      else if type = "gen" then x := -1; y := n+1; w(n)/2^n
      else if type = "ber" then x := 1; y := n+1; w(n)/(4^(n+1)-2^(n+1))
      fi fi fi fi fi
end;

Let us check the function:

types := ["eul", "tan", "spr", "gen", "ber"]:
for t in types do seq(SwissKnifeDecompositions(t,i),i=0..8) od;

From a submission to OEIS.

A154341 ==================
  
E(n,k) an additive decomposition of the Euler number 
(triangle read by rows). 

The Swiss-Knife polynomials can be understood as a sum of polynomials.
Evaluated at x=0 these polynomials result in a decomposition of the
Euler number A122045. 

Formula:
Let c(k) = frac{(-1)^{floor(k/4)}{2^{floor(k/2)}} [4 not div k].
E(n,k) = c(k)*Sum(v=0..k, (-1)^(v)*binomial(k,v)*(v+1)^n);
E(n) = Sum(k=0..n, E(n,k)).

                         1, 
                       1, -1, 
                     1, -3, 1, 
                    1, -7, 6, 0, 
                 1, -15, 25, 0, -6, 
              1, -31, 90, 0, -90, 30, 
         1, -63, 301, 0, -840, 630, -90, 
      1, -127, 966, 0, -6300, 7980, -2520, 0, 
1, -255, 3025, 0, -41706, 79380, -41580, 0, 2520, 

Maple:
E := proc(n,k) local v; if irem(k+1,4) = 0 then 0 
else (-1)^iquo(k+1,4)*2^(-iquo(k,2))*
add((-1)^v*binomial(k,v)*(v+1)^n,v=0..k) fi end: 
seq(print(seq(E(n,k),k=0..n)),n=0..8);

A154342 ==================

T(n,k) an additive decomposition of the signed tangent number
(triangle read by rows). 

The Swiss-Knife polynomials can be understood as a sum of polynomials.
Evaluated at x=1 these polynomials result in a decomposition of the
signed tangent numbers A009006. 

Formula:
Let c(k) = frac{(-1)^{floor(k/4)}{2^{floor(k/2)}} [4 not div k].
T(n,k) = c(k)*Sum(v=0..k,(-1)^(v)*binomial(k,v)*(v+2)^n);
T(n) = Sum(k=0..n, T(n,k)).

                       1, 
                     2, -1, 
                   4, -5, 1, 
                 8, -19, 9, 0, 
              16, -65, 55, 0, -6, 
          32, -211, 285, 0, -120, 30, 
      64, -665, 1351, 0, -1470, 810, -90, 
128, -2059, 6069, 0, -14280, 13020, -3150, 0, 

Maple:
T := proc(n,k) local v; if irem(k+1,4) = 0 then 0 
else (-1)^iquo(k+1,4)*2^(-iquo(k,2))*
add((-1)^v*binomial(k,v)*(v+2)^n,v=0..k) fi end:
seq(print(seq(T(n,k),k=0..n)),n=0..8);

A154343 ==================

S(n,k) an additive decomposition of the Springer number
(generalized Euler number) (triangle read by rows). 

The Swiss-Knife polynomials can be understood as a sum of polynomials.
Evaluated at x=1/2 and multiplied by 2^n these polynomials result in 
a decomposition of the Springer numbers A001586.

Formula:
Let c(k) = frac{(-1)^{floor(k/4)}{2^{floor(k/2)}} [4 not div k].
S(n,k) = c(k)*Sum(v=0..k,(-1)^(v)*binomial(k,v)*2^n*(v+3/2)^n);
S(n) = Sum(k=0..n, S(n,k)).

                                 1, 
                               3, -2, 
                            9, -16, 4, 
                         27, -98, 60, 0, 
                      81, -544, 616, 0, -96, 
                 243, -2882, 5400, 0, -3360, 960, 
          729, -14896, 43564, 0, -72480, 46080, -5760, 
    2187, -75938, 334740, 0, -1246560, 1323840, -362880, 0, 
6561, -384064, 2495056, 0, -18801216, 29675520, -13386240, 0, 645120, 

Maple:
S := proc(n,k) local v; if irem(k+1,4) = 0 then 0 
else (-1)^iquo(k+1,4)*2^(-iquo(k,2))*
add((-1)^v*binomial(k,v)*2^n*(v+3/2)^n,v=0..k) fi end:
seq(print(seq(S(n,k),k=0..n)),n=0..8);

A154344 ==================

G(n,k) an additive decomposition of 2^n*G(n), G(n) the Genocchi numbers 
(triangle read by rows). 

The Swiss-Knife polynomials can be understood as a sum of polynomials.
Evaluated at x=-1 multiplied by n+1 this results in a decomposition
of 2^n times the Genocchi numbers A036968.

Formula:
Let c(k) = frac{(-1)^{floor(k/4)}{2^{floor(k/2)}} [4 not div k].
G(n,k) = c(k)*Sum(v=0..k,(-1)^(v)*binomial(k,v)*(n+1)*v^n);
G(n) = (Sum(k=0..n, G(n,k)) / 2^n

                        1, 
                     0, -2, 
                    0, -3, 3, 
                  0, -4, 12, 0, 
                0, -5, 35, 0, -30, 
            0, -6, 90, 0, -360, 180, 
        0, -7, 217, 0, -2730, 3150, -630, 
   0, -8, 504, 0, -16800, 33600, -15120, 0, 
0, -9, 1143, 0, -91854, 283500, -215460, 0, 22680, 

Maple:
G := proc(n,k) local v, pow; 
pow := (a,b) -> if a = 0 and b = 0 then 1 else a^b fi;
if irem(k+1,4) = 0 then 0 else (-1)^iquo(k+1,4)*2^(-iquo(k,2))*
add((-1)^v*binomial(k,v)*(n+1)*pow(v,n),v=0..k) fi end:
seq(print(seq(G(n,k),k=0..n)),n=0..8);

A154345 ==================

B(n,k) an additive decomposition of (4^n-2^n)*B(n), B(n) the Bernoulli
numbers (triangle read by rows). 

The Swiss-Knife polynomials can be understood as a sum of polynomials.
Evaluated at x=1 and multiplied by n this results in a decomposition 
of (4^n-2^n) times the Bernoulli numbers A027641/A027642 (for n>0 
and B_1 = 1/2).

Formula:
Let c(k) = frac{(-1)^{floor(k/4)}{2^{floor(k/2)}} [4 not div k] 
B(n,k) = c(k)*Sum(v=0..k,(-1)^(v)*binomial(k,v)*n*(v+2)^(n-1));
B(n) = (Sum(k=0..n, B(n,k)) / (4^n-2^n)

                          1, 
                        4, -2, 
                       12, -15, 3, 
                    32, -76, 36, 0, 
                 80, -325, 275, 0, -30, 
           192, -1266, 1710, 0, -720, 180, 
        448, -4655, 9457, 0, -10290, 5670, -630, 
1024, -16472, 48552, 0, -114240, 104160, -25200, 0, 

Maple:
B := proc(n,k) local v; if irem(k+1,4) = 0 then 0 
else (-1)^iquo(k+1,4)*2^(-iquo(k,2))*
add((-1)^v*binomial(k,v)*n*(v+2)^(n-1),v=0..k) fi end: 
seq(print(seq(B(n,k),k=0..n)),n=0..8);

Some representations by the Co-Swiss-Knife polynomials:

(1) Vn(0) = 2^n Euler(n,1) for n > 0, A155585.
(2) Vn(1) = 1 - Euler(n).
(3) Vn-1(0) n / (4^n - 2^n) = B_n gives for n>1 the Bernoulli numbers A027641/A027642.
(4) Vn-1(0) n (2/2^n-2)/(2^n-1) = G_n the Genocchi number A036968 for n>1.
(5) Vn(1/2) 2^n - 1 is a signed version of the generalized Euler (Springer) numbers, see A001586.

previous Swiss-Knife polynomials

Or look it up on OEIS: Swiss-Knife decompositions

Author: Peter Luschny (2009-01-03). License: Creative Commons Attribution-ShareAlike 3.0

SK-Polynomials   Variations   Rulers   Orbitals   Factorial   Math