To the Homepage of Factorial Algorithms
To the Homepage of Factorial Algorithms
We give an overview of approximations for the factorial function, convergent or asymptotic,
old or new, compare their efficiency and give hints for their application.
Although most formulas are variations of the asymptotic expansion of James Stirling (1692–1770)
we will reach a conclusion different from those given in most places.
Some abbreviations:
kern0(n) = sqrt(2Pi/n)*(n/e)^n = kern2(n)/sqrt(n)
kern1(n) = sqrt(2Pi*n)*(n/e)^n = kern2(n)*sqrt(n)
kern2(n) = sqrt(2Pi )*(n/e)^n = sqrt(2Pi)*n^n*exp(-n) = sqrt(2Pi)*exp(n*(log(n)-1))
stieltjes0(n) : N=n+1; kern0(N) stieltjes1(n) : N=n+1; kern0(N)*exp((1/12)/N) stieltjes2(n) : N=n+1; kern0(N)*exp((1/12)/(N+(1/30)/N)) stieltjes3(n) : N=n+1; kern0(N)*exp((1/12)/(N+(1/30)/(N+(53/210)/N))) stieltjes4(n) : N=n+1; kern0(N)*exp((1/12)/(N+(1/30)/(N+(53/210)/(N+(195/371)/N)))) henrici0(n) : N=n+1; kern0(N) henrici1(n) : N=n+1; kern0(N)*exp(1/(12*N+1/N)) henrici2(n) : N=n+1; kern0(N)*exp(5/2*1/(30*N+1/N)) henrici3(n) : N=n+1; kern0(N)*exp((315*N-53/N)/(3780*N^2-510-53/N^2)) stirser0(n) : N=n+1; kern0(N) stirser1(n) : N=n+1; kern0(N)*exp(1/(12*N)) stirser2(n) : N=n+1; kern0(N)*exp(1/(12*N)*(1-1/(30*N^2))) stirser3(n) : N=n+1; kern0(N)*exp(1/(12*N)*(1-1/(30*N^2)*(1-2/(7*N^2))))
ramanujan0(n): kern1(n) ramanujan1(n): N=2*n; kern1(n)*(1+1/N)^(1/6) ramanujan2(n): N=2*n; kern1(n)*(1+1/N*(1+1/(2*N)))^(1/6) ramanujan3(n): N=2*n; kern1(n)*(1+1/N*(1+1/(2*N)*(1+1/(15*N))))^(1/6) ramanujan4(n): N=2*n; kern1(n)*(1+1/N*(1+1/(2*N)*(1+1/(15*N)*(1-11/(4*N)))))^(1/6) ramanujan5(n): N=2*n; kern1(n)*(1+1/N*(1+1/(2*N)*(1+1/(15*N)*(1-1/(4*N)*(11-79/(7*N))))))^(1/6) ______ L0(n) : kern1(n) ______ L1(n) : N=6*n; kern1(n)*(1+1/N)^(1/2) ______ L2(n) : N=6*n; kern1(n)*(1+1/N*(1+1/(2*N)))^(1/2) ______ L3(n) : N=6*n; kern1(n)*(1+1/N*(1+1/(2*N)*(1-31/(15*N))))^(1/2) ______ L4(n) : N=6*n; kern1(n)*(1+1/N*(1+1/(2*N)*(1-1/(15*N)*(31+139/(4*N)))))^(1/2) ______ L5(n) : N=6*n; kern1(n)*(1+1/N*(1+1/(2*N)*(1-1/(15*N)*(31+1/(4*N)*(139-9871/(7*N))))))^(1/2) stirling0(n) : kern1(n) stirling1(n) : N=12*n; kern1(n)*(1+1/N) stirling2(n) : N=12*n; kern1(n)*(1+1/N*(1+1/(2*N))) stirling3(n) : N=12*n; kern1(n)*(1+1/N*(1+1/(2*N)*(1-139/(15*N)))) stirling4(n) : N=12*n; kern1(n)*(1+1/N*(1+1/(2*N)*(1-1/(15*N)*(139+571/(4*N))))) nemes0(n) : kern1(n) nemes1(n) : N=12*n^2; kern1(n)*(1+1/N)^n nemes2(n) : N=12*n^2; kern1(n)*(1+1/N*(1+1/(10*N)))^n nemes3(n) : N=12*n^2; kern1(n)*(1+1/N*(1+1/(10*N)*(1+239/(21*N))))^n nemes4(n) : N=12*n^2; kern1(n)*(1+1/N*(1+1/(10*N)*(1+1/(21*N)*(239-46409/(20*N)))))^n nemesCF0(n) : kern1(n) nemesCF1(n) : kern1(n)*(n/(n-1/12*1/n))^n nemesCF2(n) : kern1(n)*(n/(n-1/12*1/(n+3/40*1/n)))^n nemesCF3(n) : kern1(n)*(n/(n-1/12*1/(n+3/40*1/(n+2369/22680*1/n))))^n nemesCF4(n) : kern1(n)*(n/(n-1/12*1/(n+3/40*1/(n+2369/22680*1/(n+7828759/10745784*1/n)))))^n
demoivre0(n) : N=n+1/2; kern2(N)
demoivre1(n) : N=n+1/2; kern2(N)*(1-1/(24*N))
demoivre2(n) : N=n+1/2; kern2(N)*(1-1/(24*N)+1/(1152*N^2))
demoivre3(n) : N=n+1/2; kern2(N)*(1-1/(24*N)+1/(1152*N^2)+(1003/414720)/N^3)
maclser0(n) : kern2(n+1/2)
maclser1(n) : N=2*n+1; kern2(n+1/2)*exp(-1/(12*N))
maclser2(n) : N=2*n+1; kern2(n+1/2)*exp(-1/(12*N)*(1-7/(30*N^2)))
maclser3(n) : N=2*n+1; kern2(n+1/2)*exp(-1/(12*N)*(1-7/(30*N^2)*(1-62/(49*N^2))))
wdsmith0(n) : N=n+1/2; kern2(N)
wdsmith1(n) : N=n+1/2; kern2(N)*exp((-1/24)/N)
wdsmith2(n) : N=n+1/2; kern2(N)*exp((-1/24)/(N+(7/120)/N))
wdsmith3(n) : N=n+1/2; kern2(N)*exp((-1/24)/(N+(7/120)/(N+(1517/5880)/N)))
wdsmith4(n) : N=n+1/2; kern2(N)*exp((-1/24)/(N+(7/120)/(N+(1517/5880)/(N+(164715/297332)/N))))
cantrell0(n) : N=n+1/2; kern2(N)
cantrell1(n) : N=n+1/2; kern2(N)/(1+1/(24*N-1/2))
cantrell2(n) : N=n+1/2; kern2(N)/(1+1/(24*N-1/2+1/((1440/2021)*N)))
cantrell3(n) : N=n+1/2; kern2(N)/(1+1/(24*N-1/2+1/((1440/2021)*N+1/((686186088/125896643)*N))))
cantrell4(n) : N=n+1/2; kern2(N)/(1+1/(24*N-1/2+1/((1440/2021)*N+1/((686186088/125896643)*N
+1/((1521596612992267104/4596084813365743279)*N)))))
lanczos0(n) : N=n+1/2; kern2(N)
lanczos1(n) : N=n+1/2; kern2(N)*(1-(1/24)*(1/(n+1)))
lanczos2(n) : N=n+1/2; kern2(N)*(1-(1/24)*(1/(n+1))-(23/1152)*(1/((n+1)*(n+2))))
lanczos3(n) : N=n+1/2; kern2(N)*(1-(1/24)*(1/(n+1))-(23/1152)*(1/((n+1)*(n+2)))
-(11237/414720)*(1/((n+1)*(n+2)*(n+3))))
wehmeier0(n) : kern2(n)*sqrt(n)
wehmeier1(n) : kern2(n)*sqrt(n+1/6)
wehmeier2(n) : kern2(n)*sqrt(n+1/6+(1/72)/n)
wehmeier3(n) : kern2(n)*sqrt(n+1/6+(1/72)/n-(31/6480)/n^2)
wehmeier4(n) : kern2(n)*sqrt(n+1/6+(1/72)/n-(31/6480)/n^2-(139/155520)/n^3)
gosper0(n) : kern2(n)*sqrt(n)
gosper1(n) : kern2(n)*sqrt(n+1/6)
gosper2(n) : kern2(n)*sqrt(n+1/6)*(1+(1/144)/n^2)
gosper3(n) : kern2(n)*sqrt(n+1/6)*(1+(1/144)/n^2-(23/6480)/n^3)
gospersmith0(n): N=n+1/2; NN=N^2; sqrt(2*Pi)*exp(-N)*(NN)^(N/2)
gospersmith1(n): N=n+1/2; NN=N^2; sqrt(2*Pi)*exp(-N)*(NN-(1/12))^(N/2)
gospersmith2(n): N=n+1/2; NN=N^2; sqrt(2*Pi)*exp(-N)*(NN+(1/12)*(-1+(1/(10*NN))))^(N/2)
gospersmith3(n): N=n+1/2; NN=N^2; sqrt(2*Pi)*exp(-N)*(NN+(1/12)*(-1+(1/(10*NN))*(1-(185/(756*NN)))))^(N/2)
luschny0(n): N=n+1/2; NN=24*N^2; kern2(N)
luschny1(n): N=n+1/2; NN=24*N^2; kern2(N)*(1-1/NN)^N
luschny2(n): N=n+1/2; NN=24*N^2; kern2(N)*(1-1/NN*(1-19/(10*NN)))^N
luschny3(n): N=n+1/2; NN=24*N^2; kern2(N)*(1-1/NN*(1-1/(10*NN)*(19-2561/(21*NN))))^N
luschny4(n): N=n+1/2; NN=24*N^2; kern2(N)*(1-1/NN*(1-1/(10*NN)*(19-1/(21*NN)*(2561-874831/(20*NN)))))^N
luschnyCF0(n): N=n+1/2; kern2(N)
luschnyCF1(n): N=n+1/2; kern2(N)*(N/(N+1/24*1/N))^N
luschnyCF2(n): N=n+1/2; kern2(N)*(N/(N+1/24*1/(N+3/80*1/N)))^N
luschnyCF3(n): N=n+1/2; kern2(N)*(N/(N+1/24*1/(N+3/80*1/(N+18029/45360*1/N))))^N
luschnyCF4(n): N=n+1/2; kern2(N)*(N/(N+1/24*1/(N+3/80*1/(N+18029/45360*1/(N+6272051/14869008*1/N)))))^N
maclstir0(n) : ( 2*maclser0(n)+ stirser0(n))/3 maclstir1(n) : ( 32*maclser1(n)+ 31*stirser1(n))/63 maclstir2(n) : ( 64*maclser2(n)+ 63*stirser2(n))/127 maclstir3(n) : (128*maclser3(n)+127*stirser3(n))/255 windschitl(n): N=n+1; sqrt(2*Pi/N)*((N/e)*sqrt(N*sinh(1/N)))^N wdsmith*(n) : N=n+1/2; sqrt(2*Pi)*((N/e)*sqrt(2*N*tanh(1/(2*N))))^N nemes*(n) : N=n; sqrt(2*Pi*N)*((N+1/(12*N-1/(10*N)))/e)^N nemesgam(n) : N=n+1; sqrt(2*Pi/N)*((N+1/(12*N-1/(10*N)))/e)^N luschny*(n) : N=n+1/2; sqrt(2*Pi)*((N-1/(24*N+19/(10*N)))/e)^N
The following table displays the number of exact decimal digits (edd) of the formulas for some values of n. Exact decimal digits are defined as -log[10](abs(1-approximation/trueValue)). log[10] denotes the logarithm to the base 10.
edd(n) = -log[10](abs(1 - approximation(n) / n!)).
In the following table the i-th entry (i=0,1,2,... from the left hand side to the
right hand side) in a line starting with 'name' is the edd of formula namei(n).
The '-' sign indicates that the approximation is smaller and the '+' sign (not
displayed) indicates that the approximation is larger than the true value.
For example we see from the table that formula nemes1 gives the same number of
exact decimal digits as the formula ramanujan2.
-----------------------------------------------------------------------
Formula n! exact decimal digits, edd(n)
-----------------------------------------------------------------------
Stirling 00100! -3.1 -6.5 8.6 11.7 -13.1
De Moivre 00100! 3.4 -7.1 -8.6 12.0 13.1
Gosper 00100! -3.1 -6.2 8.5 -11.9
Wehmeier 00100! -3.1 -6.2 8.6 11.4 -13.1
Ramanujan 00100! -3.1 -5.7 -9.2 11.0 -13.3
Nemes 00100! -3.1 -9.2 -13.2 17.3 -21.1
Luschny 00100! 3.4 -8.5 13.1 -17.2 21.1
Henrici 00100! -3.1 -8.4 -13.2 17.2
GosperSonin 00100! 3.4 -8.4 13.0 -17.2
StirSeries 00100! -3.1 8.6 -13.1 17.3
MaclSeries 00100! 3.4 -8.6 13.1 -17.2
NemesCF 00100! 3.1 8.2 13.2 17.3 21.5
Stieltjes 00100! -3.1 8.6 -13.2 17.5 -21.5
W.D.Smith 00100! 3.4 -8.6 13.2 -17.5 21.5
Cantrell 00100! 3.4 -8.6 13.2 -17.5 21.5
LuschnyCF 00100! 3.4 8.8 13.2 17.6 21.5
Windschitl 00100! -13.2
W.D.Smith* 00100! 13.2
Nemes* 00100! -13.2
NemesGamma 00100! -13.2
Luschny* 00100! 13.2
Stirling 01000! -4.1 -8.5 11.6 15.6 -18.1
De Moivre 01000! 4.4 -9.1 -11.6 16.0 18.1
Gosper 01000! -4.1 -8.2 11.4 -15.9
Wehmeier 01000! -4.1 -8.2 11.6 15.4 -18.1
Ramanujan 01000! -4.1 -7.7 -12.2 15.0 -18.3
Nemes 01000! -4.1 -12.2 -18.2 24.3 -30.1
Luschny 01000! 4.4 -11.5 18.1 -24.2 30.1
Henrici 01000! -4.1 -11.4 -18.2 24.2
GosperSonin 01000! 4.4 -11.4 18.0 -24.2
StirSeries 01000! -4.1 11.6 -18.1 24.2
MaclSeries 01000! 4.4 -11.6 18.1 -24.2
NemesCF 01000! 4.1 11.2 18.2 24.3 30.5
Stieltjes 01000! -4.1 11.6 -18.2 24.4 -30.4
W.D.Smith 01000! 4.4 -11.6 18.2 -24.5 30.5
Cantrell 01000! 4.4 -11.6 18.2 -24.5 30.5
LuschnyCF 01000! 4.4 11.8 18.2 24.6 30.5
Windschitl 01000! -18.2
W.D.Smith* 01000! 18.2
Nemes* 01000! -18.2
NemesGamma 01000! -18.2
Luschny* 01000! 18.2
Stirling 10000! -5.1 -10.5 14.6 19.6 -23.1
De Moivre 10000! 5.4 -11.1 -14.6 20.0 23.1
Gosper 10000! -5.1 -10.2 14.4 -19.9
Wehmeier 10000! -5.1 -10.2 14.6 19.3 -23.1
Ramanujan 10000! -5.1 -9.7 -15.2 19.0 -23.3
Nemes 10000! -5.1 -15.2 -23.2 31.3 -39.1
Luschny 10000! 5.4 -14.5 23.1 -31.2 39.1
Henrici 10000! -5.1 -14.4 -23.2 31.2
GosperSonin 10000! 5.4 -14.4 23.0 -31.2
StirSeries 10000! -5.1 14.6 -23.1 31.2
MaclSeries 10000! 5.4 -14.6 23.1 -31.2
NemesCF 10000! 5.1 14.2 23.2 31.3 39.5
Stieltjes 10000! -5.1 14.6 -23.2 31.4 -39.4
W.D.Smith 10000! 5.4 -14.6 23.2 -31.5 39.5
Cantrell 10000! 5.4 -14.6 23.2 -31.5 39.5
LuschnyCF 10000! 5.4 14.8 23.2 31.6 39.5
Windschitl 10000! -23.2
W.D.Smith* 10000! 23.2
Nemes* 10000! -23.2
NemesGamma 10000! -23.2
Luschny* 10000! 23.2
** The reference for the Ramanujan formula is: S. Raghavan and S. S. Rangachari (eds.) "S. Ramanujan: The lost notebook and other unpublished papers", Springer, 1988, p. 339. Ramanujan's statement is as follows:
Gamma(x+1) = Sqrt(Pi)(x/e)^x (8x^3 + 4x^2 + x + theta(x)/30)^(1/6)
where theta(x) -> 1
as x -> oo and (3/10) < theta(x) < 1.
** Paul Abbott commented Ramanujan's statement on the Usenet (sci.math.num-analysis): "For
Sqrt(Pi)*(n/E)^n*(n*(4*n*(2*n+1)+1)+(1/30)*(1-(11/(8*n))*(1-(79/(154*n))
*(1+(3539/(4740*n))*(1-(9511/(7078*n))*(1+90459/(152176*n)))))))^(1/6)
one finds that
theta(x) = 1-11/(8*x)+79/(112*x^2)+3539/(6720*x^3)-9511/(13440*x^4)-30153/(71680*x^5)
Clearly theta(x) -> 1 for x -> Infinity. Also (3/10) < theta(x) < 1 for x >~ 1.3878. So this form does agree with Ramanujan's statement."
** Michael Hirschhorn [The Mathematical Gazette, Vol. 90, July 2006, 286-292] proved the following sharper bounds for Ramanujan's theta(x), valid for x > 6053/3987 (or x > 1.52).
1 - 11/(8*x) + 5/(8*x^2) < theta(x) < 1 - 11/(8*x) + 11/(8*x^2)
** The reference for Stieltjes' continued fraction formula is: M. Abramowitz, I. A. Stegun (eds.), Handbook of Mathematical Functions, p. 258, [6.1.48]. Note also: B. W. Char: "On Stieltjes' continued fraction for the gamma function", Mathematics of Computation 34, 150 (1980) 547-551.
** There are many Lanczos formulas for approximating n!. The form we use here is his equation (21) given in "A precision approximation of the gamma function", J. SIAM Numer. Anal., Ser. B, Vol. 1 (1964), pp. 86-96. Lanczos also devised other series (not included here) which might be more useful in practical computation. So he might not be fairly represented here! (Thanks to D. W. Cantrell for this remark.)
** The formulas of Warren D. Smith were taken from The Gamma function revisited, a typeset dated 29 Mar 2006.
** The formulas cantrell and wdsmith have an almost identical numerical performance.
** In our setup the approximation of Robert H. Windschitl is only a curiosity. Warren D. Smith's formula wdsmith*(n) provides a similar approximation based on Gamma(n+1/2). The two formulas wdsmith* and windschitl bracket the true value. (Note that our interpretation of the Windschitl formula differs from the interpretation used by W. D. Smith. However, our (Gamma-) interpretation seems to be more useful.)
| z | Windschitl | z! | W.D.Smith* |
| 0.0 | 0.999658 | 1.0 | 1.00429 |
| 0.5 | 0.88617 | 0.88623 | 0.88652 |
| 1.0 | 0.999984 | 1.0 | 1.000057 |
| 1.5 | 1.329333 | 1.329340 | 1.329361 |
| 2.0 | 1.9999954 | 2.0 | 2.0000107 |
**
I do not understand why the Windschitl formula is called 'a version suitable for calculators' on
Wikipedia and other web-sides. The appearance of sinh (or tanh in the case of
wdsmith*) make them look like stars of the 'Pimp My Formula' TV-show.
Well, it is time to un-pimp these formulas and to introduce the cute nemesGamma(n) and luschny*(n)
formulas, which are much simpler but equal powerful. (For the
definitions see the paragraph Miscellaneous Approximations above.)
And there is an added value.
Comparing windschitl(n) with nemesGamma(n) we find the following approximation:
sqrt(x sinh(1/x)) = 1 + 1/(12 x^2 - 1/10) + O(x^(-6))
In fact | sqrt(x sinh(1/x)) - (1 + 1/(12 x^2 - 1/10)) | < 1 / (24192 x^6) .
Comparing wdsmith*(n) with luschny*(n) shows the approximation:
sqrt(x tanh(1/x)) = 1 - 1/(6 x^2 + 19/10) + O(x^(-6))
In fact | sqrt(x tanh(1/x)) - (1 - 1/(6 x^2 + 19/10)) | < 1 / (54 x^6) .
These two approximations are noteworthy. It does not make sense to replace the simple right hand sides by the functions on the left hand side in the above approximations to the factorial function as this will not decrease the approximation error. It will only produce pimped formulas ;-)
** Some numerical methods for computing x! (the tricks of the trade) can be found in the Handbook of Mathematical Functions (6.7).
** Let us define the Noerlund scheme as
noerlund(z,h,m)
ln(sqrt(2*Pi))+(z+h-1/2)*ln(z)-z+sum((-1)^(j+1)*bernoulli(j+1,h)/((j+1)*j*z^j),j=1..m-1)
The Noerlund scheme [Vorlesungen über Differenzenrechnung, Berlin 1924, p.111] gives us a common framework to classify approximation formulas to x!. There are three basic types, which correspond to our more general abbreviations kern#(x) used in the table above.
KERN0(x) = exp(noerlund(x+1,0,0)) = sqrt(2Pi/Y)*(Y/e)^Y where Y=x+1
KERN1(x) = exp(noerlund(x,1,0)) = sqrt(2Pi*Y)*(Y/e)^Y where Y=x
KERN2(x) = exp(noerlund(x+1/2,1/2,0)) = sqrt(2Pi)*(Y/e)^Y where Y=x+1/2
Note that KERN1 has a problem when x=0. Therefore KERN0 is to be preferred to KERN1. KERN2 has the most simple form and might be called the Hermite-Sonin variant.
** Asymptotic approximation of the Bernoulli Numbers.
Combining the nemes* formula and the well known connection of the Bernoulli Numbers with the Riemann Zeta Function we find the following remarkable formula, valid for even n >= 4.
|B(n)| ~ 2 sqrt(2 Pi n) ((n + 1/(12 n - 1/(10 n)))/(2 Pi e))^n
For example this approximation gives
| B(100) | ~ 0.28382249570691.. 10^79
compared with
| B(100) | = 0.28382249570693.. 10^79.
We can write this formula also as an approximation to Zeta(1-n), valid for even n >= 4.
| Zeta(1-n) | ~ 2 sqrt(2 Pi / n)((n / (2 Pi e))((120 n^2 + 9)/(120 n^2 - 1)))^n
The formulas given are mostly asymptotic formulas and this means they only give good approximations
if x is large. However, for small values of x there is a simple trick to overcome this shortcoming at
no great cost. Shift x in the direction -> +oo before evaluating and divide by the shifted amount afterwards.
This is, of course, nothing else but a clever application of the functional equation of x!.
I am quite fond of the continued fraction approximation of T. J. Stieltjes because of its simplicity and the small constants
involved. Note especially that this is a convergent approximation! So I built the above-mentioned trick in the
following simple function based on the stieltjes3 formula and recommend its use if only moderate precision is needed.
StieltjesFactorial(x)
y = x+1; p = 1;
while y < 7 do p = p*y; y = y+1; od;
r = exp(y*log(y)-y + 1/(12*y+2/(5*y+53/(42*y))));
if x < 7 then r = r/p fi;
return r*sqrt(2*Pi / y) end;
This approximation guarantees 9 valid decimal digits. And you can expect about 7/2+3*log(x) valid significant
decimal digits for x>=10. For programming a pocket calculator the following simplification
of the fourth line is even better suited:
r = exp(y*(log(y)-1)+1/(2*(6*y+1/(5*(y+1/(4*y))))));
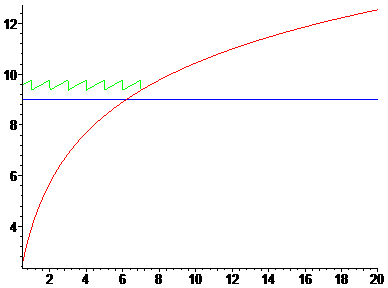
In the following plot the blue line represents the guaranteed 9 decimal digits, the
green zigzag line shows the effect of the shift/divide-trick, and the red curve is the number of exact
decimal digits of the 'pure' stieltjes3 approximation.
It is good practice to display only the valid digits of an approximation and not to leave the user more
or less helplessly looking at long strings of digits figuring out how much of these digits he might assume as valid.
However, how this is done depends much on the implementation language. I give an example using pseudo-Maple-style,
which in turn uses a formatting scheme which is very similar to the one used in the computer language 'C'.
PrintFactorial(x)
# Number of valid significant decimal digits for StieltjesFactorial.
l = floor(7/2+3*log(x));
# Put formatting specifications in the format string.
format = sprintf("%d! = %s%de\n",x,"%1.",l-1);
# Add some internal guarding digits and evaluate.
F = evalf(StieltjesFactorial(x),l+6);
printf(format, F) end;
Using this special print function to display the approximations to (2^i)!
Sequence( PrintFactorial(2^i), i = 0..12);
gives the following output, which shows only valid digits (the last digit might be rounded).
1! = 1.00e+00
2! = 2.0000e+00
4! = 2.400000e+01
8! = 4.03200000e+04
16! = 2.0922789888e+13
32! = 2.631308369337e+35
64! = 1.26886932185884e+89
128! = 3.85620482362580422e+215
256! = 8.5781777534284265412e+506
512! = 3.477289793132605363283e+1166
1024! = 5.41852879605885728307692e+2639
2048! = 1.6726919319100117051699525e+5894
4096! = 3.642736389457041931565827470e+13019
... and now we are going for the Big Pizza. The next approximation guarantees 16 valid decimal digits.
And you can expect about 5/2+(13/2)*log(x) valid significant decimal digits for x >= 10 (see the next figure).
I just give the pseudo-code because things are very similar to the things explained in the last two sections.
However, there is a small difference. This time we make explicit that we are using the logarithmic version of
the continued fraction formula. This gives an additional layer of flexibility.
StieltjesLnFactorial(z)
a0 = 1/12; a1 = 1/30; a2 = 53/210; a3 = 195/371;
a4 = 22999/22737; a5 = 29944523/19733142;
a6 = 109535241009/48264275462;
Z = z+1; (1/2)*ln(2*Pi)+(Z-1/2)*ln(Z)-Z +
a0/(Z+a1/(Z+a2/(Z+a3/(Z+a4/(Z+a5/(Z+a6/Z)))))) end;
StieltjesFactorialHP(x)
y = x; p = 1;
while y < 8 do p = p*y; y = y+1; od;
r = exp(StieltjesLnFactorial(y));
if x < 8 then r = (r*x)/(p*y) fi;
r end;
PrintFactorialHP(x)
l = floor((5+13*log(x))/2);
format = sprintf("%d! = %s%de\n",x,"%1.",l-1);
F = evalf(StieltjesFactorialHP(x),l+6);
printf(format, F) end;
1! = 1.00e+00
2! = 2.000000e+00
4! = 2.4000000000e+01
8! = 4.032000000000000e+04
16! = 2.0922789888000000000e+13
32! = 2.631308369336935301672180e+35
64! = 1.2688693218588416410343338934e+89
128! = 3.856204823625804217356770659234637e+215
256! = 8.5781777534284265411908227168123262516e+506
512! = 3.477289793132605363283045917545604711992251e+1166
1024! = 5.4185287960588572830769219446838547380015539636e+2639
2048! = 1.672691931910011705169952468793676234018507002356737e+5894
4096! = 3.6427363894570419315658274703116469205712449235098554300e+13019
Note: This paragraph was written before I discovered the 'luschnyCF' formulas
and is not up-to-date.
The Stirling formula is a very useful formula when we have to do some Big-O
(complexity-) analysis. But if we are only interested in the numerical
evaluation of the factorial function then there is no reason to use the Stirling approximation or some
of its many asymptotic variants. Because there exist convergent approximations which are
In our judgement there are three outstanding formulas which we declare the winners of our little contest.
Clearly the continued fraction of W. D. Smith is a variant of Stieltjes' formula. And the coefficients
of this formula are slightly larger than those of the Stieltjes formula. Another
runner-up is Cantrell's formula, which is numerically on par with Smith's
formula but has even larger rational constants (which does not really matter if
we are using floating point arithmetic with fixed precision). Note that we
looked only at the real range x > 1. If considered throughout the complex half-plane Re(z)
> 1 there might be some special strength or weakness in the formulas which we
have not noticed.
Summa summarum we highly recommend Stieltjes' formula whenever a numerical approximation of the
factorial function is required.
=> A000207 at OEIS.
Recently Rainer Rosenthal drew my attention to the number of planar 2-trees, sequence A000207 at OEIS.
The sequence can be computed as (Maple):
A000108 := n -> (2*n)! / (n!*(n+1)!);
A000207 := n -> A000108(n)/(2*n+4)+A000108(floor(n/2))*(3-modp(n,2))/4 +`if`(modp(n,3)=1,A000108(floor((n-1)/3))/3,0);
I noticed that the quotient A000207(n+1) / A000207(n) has a remarkable
regular asymptotic expansion:
QuotAsymptotic := n -> 4 - (10/n)*(1-(3/n)*((1-(3/n)*((1-(3/n)*((1-(3/n)
*((1-(3/n)*((1-(3/n)*((1-(3/n)))))))))))))).
=> Update Jan 11, 2007: The computation of Stieltjes' continued fraction.
After calculating his famous continued fraction for the Gamma function Stieltjes remarked: "Le calcul est trés pénible ... la loi de ces nombres paraît extrêmement compliqué". I looked at the state of the art and wrote a summary. See the link list below.
=> Update Jan 9, 2007: Two new continued fraction approximations added.
My latest additions are the formulas luschnyCT and nemesCT. A first comparison shows that the luschnyCT formula performs slightly better than Stieltjes' formula (or the W.D.Smith or Cantrell formula).
=> Update Jan 4, 2007: Three simple but powerful formulas added.
The formulas nemes*, nemesGamma and luschny* are new. They are much simpler than the windschitl or wdsmith* formulas but equal powerful.
=> Update Dec 28, 2006: The Luschny formulas added.
The new Luschny formulas added following Sonin's 'half-shift' idea and similar to the Nemes approach.
=> Update Dec 14, 2006: The Gosper-Smith formulas added.
Gosper's z! ~ sqrt((2*z+1/3)*Pi)*(z/e)^z recasted by W. D. Smith following Sonin's 'half-shift' idea.
=> Update Dec 13, 2006: Warren D. Smith's formulas added.
The continued fraction formulas of W. D. Smith are based on the Hermite-Sonin discussion: Sur les polynômes d'Bernoulli, Extrait d'une correspondance entre M. Sonin et M. Hermite. J. für Math. 116 (1896), 133-156.
=> Update Nov 18, 2006: The Continued Fraction Formula corrected
Gergö Nemes spotted an error in stieltjes3. Thanks, Gergö! With this correction, the author hopes that the formulas are now error-free.
=> Update Nov 12, 2006: The Nemes Formula announced
Gergö Nemes, a student from Hungary, sent me his formula. Thank you Gergö for sharing your findings with us!
 |
=> Update Nov 9, 2006: The Wehmeier Formula rediscovered
 |
In expanded normal form:
 |
First I thought that I had discovered a new family of formulas. However, a closer examination showed that I had rediscovered the Wehmeier formula while I was contemplating the Ramanujan formula. Nevertheless, I left the L-formula in the table because I think this alternative way to look at the Wehmeier formula throw some light on the structure of the Ramanujan formula.
=> Update Aug, 2006: S. Ramanujan's Formula
 |
In expanded normal form:
 |
Back to the Homepage of Factorial Algorithms.
